An Introduction to 3D Gaussian Splatting Fundamentals

by kyjohnso

A comprehensive introduction to the mathematical foundations and core concepts behind 3D Gaussian Splatting technology.

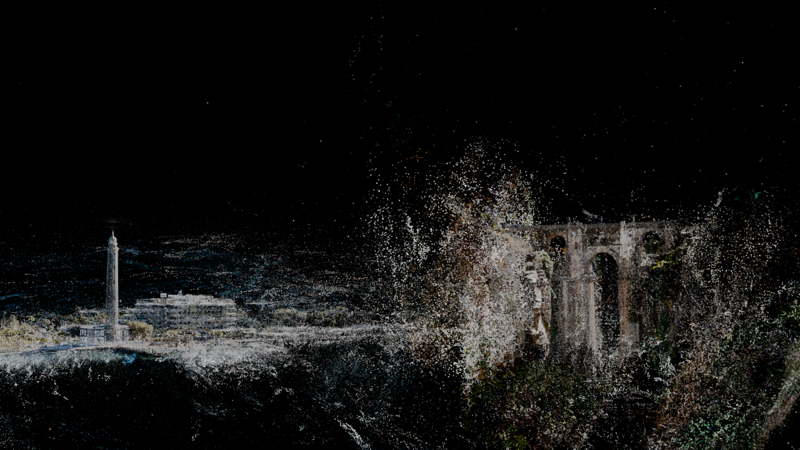
3D Gaussian Splatting Point Cloud Visualization 3D Gaussian Splatting Point Cloud Visualization

3D Gaussian Splatting (3DGS) represents a paradigm shift in how we approach real-time rendering of photorealistic 3D scenes. This article explores the mathematical foundations and core concepts that make this technology so powerful.

What Makes 3DGS Different?

The idea of 3DGS is actually not new, though it has gained in popularity in the last 2 years.

Key Advantages

  • Real-time Performance: Renders at interactive frame rates
  • Photorealistic Quality: Maintains high visual fidelity
  • View-dependent Effects: Naturally handles reflections and lighting
  • Efficient Storage: Compact representation of complex scenes

Mathematical Foundation

3D Gaussian Functions

At its core, each Gaussian splat is defined by:

\[ G(\mathbf{x}) = \exp\left(-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right) \]

Where:

  • \(\boldsymbol{\mu}\) is the 3D position (mean)
  • \(\boldsymbol{\Sigma}\) is the 3×3 covariance matrix
  • \(\mathbf{x}\) is any point in 3D space

Covariance Matrix Decomposition

The covariance matrix \(\boldsymbol{\Sigma}\) is decomposed into:

\[ \boldsymbol{\Sigma} = \mathbf{R} \mathbf{S} \mathbf{S}^T \mathbf{R}^T \]

Where:

  • \(\mathbf{R}\) is a rotation matrix (3×3)
  • \(\mathbf{S}\) is a scaling matrix (3×3 diagonal)

This decomposition allows independent control over:

  • Position (\(\boldsymbol{\mu}\)): Where the Gaussian is located
  • Rotation (\(\mathbf{R}\)): How it’s oriented in space
  • Scale (\(\mathbf{S}\)): Its size along each axis

Spherical Harmonics

Color information is encoded using spherical harmonics (SH), allowing view-dependent appearance:

\[ C(\mathbf{d}) = \sum_{l=0}^{L} \sum_{m=-l}^{l} c_l^m \cdot Y_l^m(\mathbf{d}) \]

Where:

  • \(\mathbf{d}\) is the viewing direction
  • \(c_l^m\) are the SH coefficients
  • \(Y_l^m\) are the spherical harmonic basis functions

Rendering Pipeline

1. Projection to 2D

Each 3D Gaussian is projected to screen space using the camera parameters:

\[ \boldsymbol{\Sigma}' = \mathbf{J} \mathbf{W} \boldsymbol{\Sigma} \mathbf{W}^T \mathbf{J}^T \]

Where:

  • \(\mathbf{J}\) is the Jacobian of the projection
  • \(\mathbf{W}\) is the world-to-camera transformation

2. Alpha Blending

Gaussians are sorted by depth and blended using:

\[ C = \sum_{i=1}^{N} c_i \cdot \alpha_i \cdot \prod_{j=1}^{i-1} (1 - \alpha_j) \]

Where:

  • \(c_i\) is the color of Gaussian i
  • \(\alpha_i\) is its alpha value
  • The product term handles occlusion

3. Optimization

The system is trained end-to-end using gradient descent on:

\[ \mathcal{L} = \mathcal{L}_{\text{color}} + \lambda_{\text{ssim}} \cdot \mathcal{L}_{\text{ssim}} \]

Where:

  • \(\mathcal{L}_{\text{color}}\) is the L1 color loss
  • \(\mathcal{L}_{\text{ssim}}\) is the structural similarity loss
  • \(\lambda_{\text{ssim}}\) balances the two terms

Implementation Considerations

Memory Management

Each Gaussian requires storage for:

  • Position: 3 floats (12 bytes)
  • Rotation: 4 floats (16 bytes, quaternion)
  • Scale: 3 floats (12 bytes)
  • Opacity: 1 float (4 bytes)
  • SH coefficients: 48 floats (192 bytes, degree 3)

Total: ~236 bytes per Gaussian

GPU Optimization

Efficient rendering requires:

  • Tile-based rendering: Divide screen into tiles
  • Frustum culling: Skip invisible Gaussians
  • Level-of-detail: Reduce complexity at distance
  • Memory coalescing: Optimize GPU memory access

Practical Applications

Scene Reconstruction

3DGS excels at reconstructing scenes from:

  • Multi-view photographs
  • Video sequences
  • LIDAR point clouds
  • Photogrammetry data

Real-time Rendering

Applications include:

  • Virtual Reality: Immersive environments
  • Gaming: Photorealistic backgrounds
  • Architecture: Walkthrough visualizations
  • Film: Digital set extensions

Limitations and Challenges

Current Limitations

  • Dynamic scenes: Limited support for moving objects
  • Transparency: Complex transparent materials are challenging
  • Editing: Difficult to modify reconstructed scenes
  • Storage: Large datasets require significant memory

Active Research Areas

  • Temporal consistency: Handling video sequences
  • Semantic understanding: Object-level editing
  • Compression: Reducing storage requirements
  • Hybrid approaches: Combining with traditional rendering

Getting Started with 3DGS

Tools and Software

  • Original Implementation: 3D Gaussian Splatting
  • SkySplat Blender: Our Blender integration
  • Viewers: Web-based and standalone viewers
  • Conversion Tools: Format converters and utilities

Learning Resources

Conclusion

3D Gaussian Splatting represents a fundamental shift in 3D rendering technology. By understanding its mathematical foundations and implementation details, developers and artists can better leverage this powerful technique for their projects.

The combination of real-time performance and photorealistic quality makes 3DGS particularly exciting for interactive applications, while its efficient representation opens new possibilities for content creation and distribution.

As the technology continues to evolve, we can expect to see even more innovative applications and improvements in the coming years.

Want to dive deeper? Try the SkySplat Blender addon to start experimenting with 3DGS today.